Pre-digital Calculating, Filing & Weather Forecasting

Log tables for multiplying and dividing

Log tables and antilog tables were the only way to multiply and divide large numbers quickly, easily and accurately before today's electronic calculators. The only alternatives were slide rules which were easy to use but not reliably accurate; mechanical calculating machines which were slow and fiddly; and what was called long multiplication and division which was based on slow and clumsy mental arithmetic. This page explains what logarithms are and how to work with them using log tables and antilog tables. The relationship with log scales is included. Highlights are the recollections from people who worked with logarithms as a norm.

____

By the webmaster, based childhood experience and additional research

Logarithms: what they are and how they work

Logarithms provide an easy means of multiplying and dividing using just simple addition and subtraction together with lookup tables.

Let me explain how they work. We all know that 10  x  100 = 1000.

Expressed in powers of ten this can be written as:

10¹ x 10² = 10³

which could also be written more generally as

10^x x 10^y = 10^x+y

These powers of 10 i.e. the x and y, are called logarithms, or more specifically base 10 logarithms or logarithms to the base ten. There are other bases, but there is no need to go into that here.

As an example, suppose you want to multiply 2 by 5. Yes, you know the answer anyway, but the explanation is easiest with a simple example.

The base 10 logarithm of 2 happens to be 0.301. Please just accept that for the moment. It means that 10^0.301 = 2

The base 10 logarithm of 5 is 0.699, which means that 10^0.699 = 5

So 2 x 5 = 10 could be written as

10^0.301 x 10^0.699 = 10 ^{0.301 + 0.699} = 10¹

or more generally:

A x B = 10^log(A) x 10^log(B) = 10^{log(A)+log(B)}

Similarly for division:

A / B = 10^log(A) / 10^log(B) = 10^{log(A)-log(B)}

From this, you can see that of you can look up the logs of numbers, add or subtract them and then decode the result, the maths is very much easier for multiplying and dividing large numbers. This is where log tables and antilog tables come in - see below.

John Napier and the first log and antilog tables

John Napier was a Scottish mathematician working back in the 17th century. He was the first person to recognise the huge advantage of logarithms. He undertook the enormous task of working out the logarithms and antilogarithms of numbers to the base 10 and he published them as a book in 1614.

Log and antilog tables in schools

Log and antilog tables were introduced into schools in 1908 when a Mr Castle published them in his book. This was not only before electronic calculators but also well before the UK went decimal, which meant that many calculations were not as straightforward as they are today.

The books, sometimes called logarithmic tables or logarithm tables were provided in school maths classes and were essential for the maths examination known as 'Ordinary Level' or just 'O level*'.

Godfrey and Siddons Four Figure Tables, as used in schools in 1950s UK

I started using these tables in the 1950s at my grammar school. Those that my school provided at that time were by Godfrey and Siddons, and published by Cambridge University Press. They were somewhat thin booklets which were easy to carry around and must have been relatively cheap for schools to buy. If you are old enough, you will recognise the photo.

These Godfrey and Siddons books of tables were accurate to four figures and accordingly had the title of Four Figure Tables on the front. However, similar tables did exist to more than four figures although I never saw any of them at the time. There were other authors and publishers.

As our main use of these tables was for looking up logarithms and antilogarithms as a means of multiplying and dividing, they acquired the name of Log Tables or just Logs, even though they did contain other types of mathematical tables.

How the log and antilog tables worked:

All that mattered for users and ordinary school children at the time was that two or more numbers could be multiplied together by adding their logs - obtained from our log tables - and then decoding the result from our antilog tables. Similarly a number could be divided by a second number by subtracting the log of the second number from the log of the first number and then decoding it from the antilog tables,

Decimal points and powers of ten

Like slide rules, log tables do not show where to place a decimal point in an answer or if any zeros are necessary before or after the answer. To find this out, a rough calculation is necessary as explained on the slide rule page.

How to use log tables and antilog tables

The following image shows the row and column structure of a typical page of a log table. The image is intentionally too small for the individual numbers to be legible, because the purpose here is only to show the 'shape' or structure of a page. This is important for understanding how the table was used.

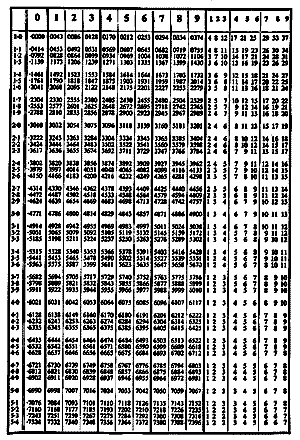
Row and column structure of a page of logarithms in a book of Four Figure Tables.

How to find the log of a number

In the left-hand column are numbers from 10, through to 99 (which actually requires more than one page). The logs of these numbers are in the adjacent column which has the heading 0. So for example if you want the log of, say, 34 (or 3.4 or 3400 because finding the decimal point is a separate operation), find 34 in the left hand column. Its log is next to it in the column headed 0.

If, though, you wanted the log of 347 (or 3.47 or 24700 etc), the log would be further to the right in the 7 column.

If you wanted the log of a four figure number, like 3476 you would go the wide column at the extreme right, find the number under the 6 heading and add that to the log of 347.

A ruler was essential to prevent wandering off one row and onto another, but the layout does make this more manageable by having a blank between every third row.

To multiply two or more numbers together, just find their logs and add them together to get the combined log. If this came to more than four figures, it was shortened to four figures, up one or down one in the fourth figure depending on whether the fifth figure was more or less than 5. Then find their antilogs - see below.

To divide one number by another, just subtract their logs and then antilog.

How to find the antilog of a number

Antilogarithms enable the sum or subtraction of logs to be decoded back to the answer of the multiplication or division. Having found the log of the multiplication or division, that number was looked up in the book's antilog tables, using the procedure explained above. The position of any decimal point was established as explained on the slide rule page.

The result, or the answer, was correct to four significant figures, but to be sure, it was usually shortened to three significant figures.

The pros and cons of using logarithms for multiplication and division

This use of logarithms may seem longwinded by today's standards where electronic calculators are widely available, but you need to realise that the additions and subtractions involved were not particularly arduous for us. Because there were no electronic calculators most people became adept at what was called 'mental arithmetic' and it was taught as a school subject to young children. My father, for example, who worked with figures all his life, could glance so rapidly down a column of complex numbers, that it looked as if he was simply checking that they were legible. Then he could immediately announce what they added up to.

So to us, before we knew anything about electronic calculators, logarithms were all advantages with no disadvantages. There was nothing that we knew of that could possibly make multiplication and division of large numbers any easier. We were of course taught how to multiply and divide large numbers using only pen and paper and what were known as 'long multiplication' and 'long division', but these methods were unwieldy and open to far more errors than looking up numbers in tables and simply adding, subtracting and decoding in antilogs.

Log scales

On any normal numerical scale, the distance between integers (whole numbers) is the same. If anyone of my young generation had been interested in making a scale showing log 10, log20, log 30 etc, we would have found that the higher the number, the more scrunched up the scale would become. Each value is greater than the earlier one but by a progressively smaller amount. The result is called a log scale.

Log scales have uses where the breadth of the data is very large, so that a regular ruler or measure would have to be uncontrollably long. Slide rules work on the principle of log scales. In the following image, the top scale is uniform with the same space between the integers 1 - 5, but the scale just below is a log scale with the numbers scrunched up close together. There is also what is effectively an antilog scale, but there more explanation on the slide rule page.

Log scale (second scale down from the top) on a slide rule.

Log scales have uses in finance, astronomy and in any graphical display of large amounts of data where it helps to visualise trends. It must be remembered, though, that log scales give the logs of any number, not the number itself. This is not always realised by the general public which gives rise to misleading interpretations - in some cases intentionally so.

___

* The General Certificate of Education Ordinary Level exam (also known as the GCE O Level) was the precursor of GCSEs and introduced in Britain in the 1950s.

sources: early 20th century material      sources: ww2 home front and other material     contact
the webmaster/author/researcher/editor     privacy policy

---

---